class AdalineSGD(object):
def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=1):
self.eta=eta
self.n_iter=n_iter
self.w_initialized=False
self.shuffle=shuffle
self.random_state=random_state
def fit(self, X,y):
self._initialize_weights(X.shape[1])
self.cost_=[]
for i in range(self.n_iter):
if self.shuffle:
X,y=self._shuffle(X,y)
cost=[]
for xi, target in zip(X,y):
cost.append(self._update_weights(xi,target))
avg_cost=sum(cost)/len(y)
self.cost_.append(avg_cost)
return self
def partial_fit(self, X, y):
if not self.w_initialized:
self._initialize_weights(X.shape[1])
if y.ravel().shape[0]>1:
for xi, target in zip(X,y):
self._update_weights(xi,target)
else:
self._update_weights(xi,target)
return self
def _shuffle(self, X, y):
r=self.rgen.permutation(len(y))
return X[r],y[r]
def _initialize_weights(self, m):
self.rgen=np.random.RandomState(self.random_state)
self.w_=self.rgen.normal(loc=0.0, scale=0.01, size=1+m)
def _update_weights(self, xi, target):
output=self.activation(self.net_input(xi))
error=(target-output)
self.w_[1:]+=self.eta*xi.dot(error)
self.w_[0]+=self.eta*error
cost=0.5*error**2
return cost
def net_input(self, X):
return np.dot(X,self.w_[1:])+self.w_[0]
def activation(self,X):
return X
def predict(self, X):
return np.where(self.activation(self.net_input(X))>=0.0, 1, -1)
import numpy as np
X_std=np.copy(X)
X_std[:,0]=(X[:,0]-X[:,0].mean())/X[:,0].std()
X_std[:,1]=(X[:,1]-X[:,1].mean())/X[:,1].std()
ada=AdalineSGD(n_iter=15, eta=0.01, random_state=1)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Stochastic Gradient Descent')
plt.xlabel('sepal length[standardized]')
plt.ylabel('petal length[standardized]')
plt.legend(loc='upper left')
plt.show()
plt.plot(range(1, len(ada.cost_) +1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Eaverage Cost')
plt.tight_layout()
plt.show()

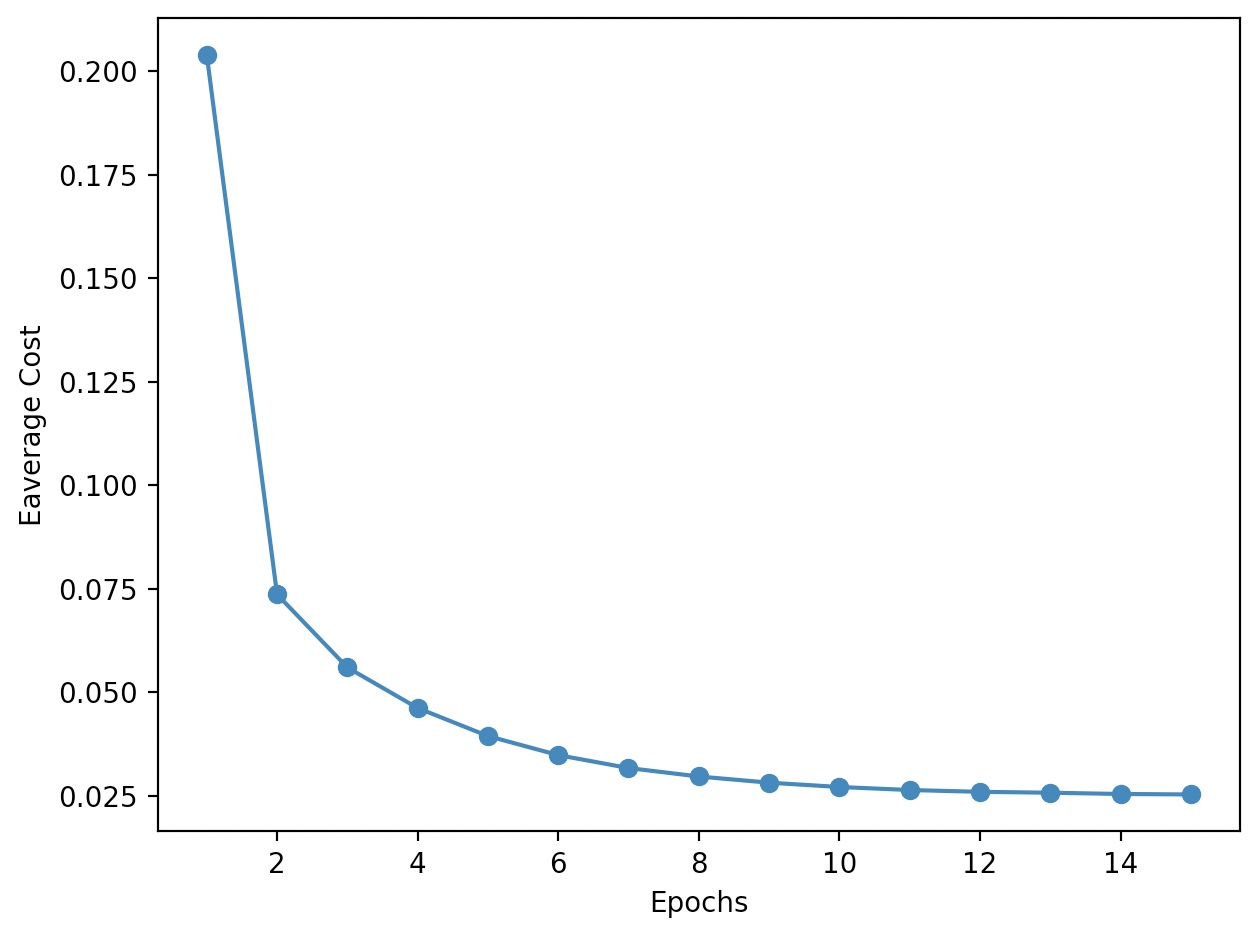
평균 비용이 상당히 빠르게 감소한다. 15번째 에포크 이후 최종 결정 경계는 배치 경사 하강법과 유사
partial_fit 메서드를 이용하여 온란인 학습 방식으로 모델을 훈련할 수 있다.
ada.partial_fit(X_std[0,:], y[0])